대수 구조 군(Group), 환(Ring), 체(Field) 이해하기

 추상 대수학에서 대수 구조(Algebraic structure)는 일련의 연산들이 주어진 집합으로, 이러한 대수 구조들 중 보안 분야에서의 암호학을 이해하기 위해서는 군(Group), 환(Ring), 체(Field)의 성격을 이해할 필요가 있습니다.

군 (Group)

군은 다음 네 가지 성질을 만족하는 이항 연산 $\bullet$이 정의된 원소들의 집합을 의미합니다. 여기서 연산 $\bullet$은 아직은 정의되지 않은 어떤 연산을 추상적으로 표현한 것이라고 이해하시면 됩니다.

 

군의 성질

1. 닫혀있음(Closure)

집합 $\mathbb{G}$에 속하는 임의의 두 원소 $a, b$에 대해 $c = a \bullet b$에서 $c$도 $\mathbb{G}$의 원소일 때, "$\mathbb{G}$는 연산 $\bullet$에 대하여 닫혀있다."라고 합니다. 연산 $\bullet$의 모든 결과 또한 집합 $\mathbb{G}$에 포함된다는 의미입니다.

 

2. 결합법칙(Associativity)

집합 $\mathbb{G}$에 속하는 임의의 세 원소 $a, b, c$에 대해 $(a \bullet b) \bullet c = a \bullet (b \bullet c)$를 만족하는 성질입니다. 동일한 연산인 경우 우선순위와 상관 없이 결과가 동일함을 의미합니다.

 

3. 항등원 존재(Existence of Identity)

집합 $\mathbb{G}$에 속하는 임의의 원소 $a$에 대해 $e \bullet a = a \bullet e = a$를 만족하는 항등원 $e$가 존재하며 $e$ 또한 집합 $\mathbb{G}$에 속하는($e \in \mathbb{G}$) 성질입니다. 항등원은 임의의 수 $a$에 대해 어떤 수를 연산했을 떄 처음의 수 $a$가 만들어 주는 수를 의미합니다.

 

4. 역원 존재(Existence of Inverse)

집합 $\mathbb{G}$에 속하는 임의의 원소 $a$에 대해 $a \bullet a' = a' \bullet a = e$를 만족하는 역원 $a'$가 존재하며 집합 $\mathbb{G}$에 속하는($a' \in \mathbb{G}$) 성질입니다.

위의 네 가지 성질에서 다음의 다섯 번째 성질을 추가로 만족하는 경우 해당 집합을 가환군(Commutative Group) 혹은 아벨 군(Abelian Group)이라고 합니다.

5. 교환 법칙(Commutativity)

집합 $\mathbb{G}$의 임의의 원소 $a, b$에 대해 $a \bullet b = b \bullet a$를 만족하는 성질입니다.

 

증명하기

예를 들어 $(\mathbb{Z}_{5}, +)$가 군임을 보이기 위해서는 위의 4가지 성질이 만족하는지 확인해야 합니다. 여기서 $\mathbb{Z}_{5} = \{0, 1, 2, 3, 4\}$이며 연산 $+$는 모듈로 5에서의 덧셈 연산이라고 정의하겠습니다. 정수의 표현에 대해 잘 모르시는 분들은 다음 페이지를 참고하세요.

 

정수 집합의 표현

자! 이제 $(\mathbb{Z}_{5}, +)$이 군의 성질 4가지를 만족하는지 보겠습니다.

1. 닫혀있음(Closure)

집합 $(\mathbb{Z}_{5}$에 속하는 임의의 두 원소에 대해 $+$ 연산한 결과가 집합 $(\mathbb{Z}_{5}$에 속하는지 확인합니다.

$0 + 0 \equiv 0 (mod 5)$

$0 + 1 \equiv 1 (mod 5)$

$0 + 2 \equiv 2 (mod 5)$

$0 + 3 \equiv 3 (mod 5)$

$0 + 4 \equiv 4 (mod 5)$

...

$4 + 0 \equiv 4 (mod 5)$

$4 + 1 \equiv 0 (mod 5)$

$4 + 2 \equiv 1 (mod 5)$

$4 + 3 \equiv 2 (mod 5)$

$4 + 4 \equiv 3 (mod 5)$

임의의 두 원소에 대해 $+$ 연산한 결과가 모두 집합 $(\mathbb{Z}_{5}$에 포함됨으로 닫혀있습니다.

여기서 $\equiv$는 Modulo 연산에서의 합동을 의미합니다.

 

2. 결합 법칙(Associativity)

집합 $(\mathbb{Z}_{5}$에 속하는 임의의 세 원소가 $+$ 연산에 대해 결합 법칙을 만족하는지 봅니다.

$(0 + 1) + 2 \equiv 0 + (1 + 2) \equiv 0 + 1 + 2 (mod 5)$와 같이 어떠한 세 원소에 대해 결합해도 결과는 모두 합동임으로 결합법칙 성질을 만족합니다.

 

3. 항등원 존재(Existence of Identity)

집합 $\mathbb{Z}_{5}$에 속하는 임의의 원소가 $+$ 연산에서 항등원이 존재하는지 봅니다. 예를 들어 원소 1에 대해 항등원이 존재하는지 보면 $1 + 0 = 0 + 1 = 1$로 항등원 0이 존재하며 0은 $(\mathbb{Z}_{5}$에 속합니다. 따라서 항등원이 존재합니다.

 

4. 역원 존재(Existence of Inverse)

집합 $\mathbb{Z}_{5}$에 속하는 임의의 원소가 $+$ 연산에서 항등원을 만들 수 있는 역원이 존재하는지 봅니다. 예를 들어 원소 1에 대해 항등원 0을 만들 수 있는 역원은 4입니다. $1 + 4 = 0 (mod 5)$이기 때문입니다.

따라서 $(\mathbb{Z}_{5}, +)$는 군이 될 수 성질을 모두 만족하기 때문에 군입니다. ^^

환 (Ring)

군은 하나의 연산에 대해 군에서 만족해야 하는 성질을 만족하는 집합을 의미하지만, 환은 2개의 연산이 정의된 대수 구조로 환($\mathbf{R}$)은 $\mathbf{R} = <...,\bullet,\square>$로 표현합니다. 환의 첫 번째 연산인 $\bullet$은 가환군에 요구되는 5가지 성질을 모두 만족해야 하며, 두 번째 연산 $\square$는 군의 1, 2번 성질만 만족하거나 첫 번째 연산에서 분배 법칙(Distributivity) 성질을 추가로 만족해야 합니다. 분배 법칙은 $a \square (b \bullet c) = (a \square b) \bullet (a \square c)$와 $(a \bullet b) \square c = (a \square c) \bullet (b \square c)$를 만족하는 것입니다.

예를 들어 $\mathbf{R} = <\mathbb{Z},+,\times>$일 때 모든 정수에 대한 덧셈은 가환군의 5가지 성질을 만족하고, 곱셈은 첫 번째 덧셈 연산 위에 분배 법칙을 만족하기 때문에 가환환의 성질을 만족합니다.

체 (Field)

체($\mathbf{F}$)는 $\mathbf{F}=<{...},\bullet,\square>$로 표현하며 체는 주어진 두 개의 연산이 모두 가환환으로 군의 5가지 성질을 모두 만족하는 대수 구조를 의미합니다. 체는 수학에서 사용되는 덧셈과 뺄셈, 곱셈과 나눗셈 연산의 두 쌍들을 모두 사용할 수 있는 구조가 됩니다. 물론 0으로 나누는 것은 제외합니다.

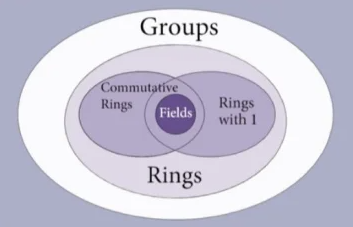
유한 체(Finite Field)

체(Field) 중에 유한체는 유한개의 원소를 갖는 체(F)로 암호에서 가장 중요한 대수 구조입니다. 수학자 갈루아는 유한개의 원소를 갖는 체에 대해 원소의 개수가 $p^n$임을 보였습니다. 여기서 $p$는 소수이고 $n$은 양의 정수입니다. 이러한 유한체를 보통 갈루아 체(Galois Field)라고 부르며 $GF(p^n)$로 표현합니다.

갈루아 체 $GF(p^n)$는 $p^n$개의 원소를 갖는 유한체입니다.

암호학에서는 이런 유한개의 원소 내에서 정의된 연산을 사용하여 암호화와 복호화 연산을 구현합니다.

 

소수 체(Prime Field)

유한체 $GF(p^n)$ 에서 $n = 1$인 유한 체를 소수체라고 하며, 원소는 $\{0, 1, 2, ..., p-1\}$이 됩니다. 예를 들어 AES연산에서 중요한 소수체는 $GF(2) = \{0, 1\}$입니다. $GF(2)$에서 덧셈은 XOR연산과 동일하고 곱셈은 논리적 AND 연산과 동일합니다.

확장 체(Extension Field)

암호학에서는 덧셈, 뺄셈, 곱셈, 나눗셈의 네 개의 연산을 필요로하기 때문에 체(Field)를 사용합니다. 체의 대수구조를 사용할 때 다음의 2가지 경우를 고려할 수 있습니다.

1. $2^n$보다 작은 수 중에 가장 큰 소수 $p$를 이용하여 $\mathbb{Z}_{p}$에 정의된 $GF(p)$를 사용
2. 원소의 개수가 $2^n$인 $GF(2^n)$ 체를 사용

첫 번째의 경우, p로부터 $2^n - 1$까지의 정수들은 사용할 수 없기 때문에 비효율적입니다. 두 번째의 경우는 $2^n$이 소수가 아니기 때문에 소수체로 사용할 수는 없습니다. 소수가 되어야 집합은 $\mathbb{Z}_{p} = \{0, 1, 2, ..., (p-1)\}$이 될 수 있으며, 이 집합에서 각각의 원소들은 덧셈 역원과 0이 아닌 원소에 대한 곱셈 역원을 가질 수 있어서 사칙연산이 가능합니다.

따라서 $GF(2^n)$이 사칙연산이 가능하도록 새로운 연산을 정의한 체가 확장 체입니다.

예를 들어 2비트 워드로 구성된 집합 $\{00, 01, 10, 11\}인 $GF(2^2)$는 다음과 같이 연산을 정의할 수 있으며, 덧셈은 XOR연산으로 사용할 수 있고 곱셈은 2비트가 넘는 경우 1의 보수를 취하여 0을 제외한 곱셈에 대한 항등원을 만들어 줄 수 있습니다. 덧셈과 곱셈에 대한 항등원이 있다는 것은 각 연산의 역원을 구할 수 있다는 의미입니다.

확장 체에서의 덧셈과 곱셈 (연두색은 항등원)

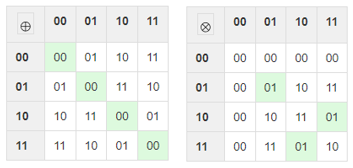
예를 들어 곱셈 10 x 10은 100이지만 2비트를 넘어서기 때문에 1의 보수를 취하여 11이 됩니다. 곱셈 연산에서 11과 10을 곱하면 01로 항등원 1이 됩니다. 이 말은 11에 어떤 곱셈을 한 후 10을 곱하면 곱한 수를 구할 수 있다는 의미입니다. 예를 들어 11에 임의의 수11을 곱하면 10이 됩니다. 결과값 10에 11의 항등원 10을 곱하면 11이 나옵니다. 여기서 11은 임의로 곱해진 수입니다. ^^; A x 3 = 3A일때 A의 역원 즉 곱셈의 항등원으로 만들어 주는 수 A'를 곱하면 3AA' = 3 x 1이 되어 3이 나온다는 의미입니다. 이렇게 컴퓨터 연산에서는 확장체를 정의하여 덧셈, 빼셈, 곱셈, 나눗셈의 사칙연산을 수행합니다.